The fourth week in April is an important one for drone enthusiasts. First, April 22–25, AUVSI (Association for Uncrewed Vehicle Systems International) co-hosts the Xponential conference and exhibition. Global leaders and end users in the uncrewed systems and robotics industry will gather
…Blog Posts
The saying “in like a lion out like a lamb” is most often used for March, but April can also be a crazy weather month. While aviation training tends to focus on the go/no-go decision, equally critical are the continue/divert decisions that happen quite literally throughout
…For the past several years, the FAA has been working on an update for the Airman Certification Standards (ACS) and Practical Test Standards (PTS). Monday, using a process called incorporation by reference (IBR), Parts …
If you’re a remote pilot, you should know that March 16, 2024, is an important date regarding the enforcement of Remote ID for drones. The FAA has been working to safely and securely integrate UAS (uncrewed aircraft systems) into the national airspace system. This has included a move toward drones
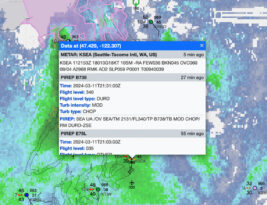
…Some of the most important jargon you’ll learn as a pilot has to be how to read a METAR. These “aviation routine weather reports” provide pilots with an accurate depiction of current weather conditions at an airport. METARs are issued on a regularly scheduled basis, usually close to the top
…The past few weeks have seen extraordinary weather events in all parts of the United States. Unusually cold temperatures have brought everything from ice storms to blizzards, even in places that don’t usually expect white winters. Pilots must keep the weather in mind when preparing for any flight. You can
…If you hang out around aviation enthusiasts, you may have heard the term mosaic a whole lot more often in recent months. What is this term and how does it apply to you? No bits of ceramic are used to make art in this type of MOSAIC. It stands for
…Want to be sure your flightpath is clear on Christmas Eve? Don’t worry, NORAD has you covered. Early in the morning on December 24th, NORAD (the North American Aerospace Defense Command) records the launch of a very special aircraft. After coordinating with “Santa’s Elf Launch Staff” to confirm his launch
…