Today, we’ll introduce airplane stability. As you’re well aware of by now, there are three axes around which the airplane moves (yaw, pitch, and roll). These axes pass through the airplane’s center of gravity, or the point where the airplane weight is considered to be concentrated. An airplane that is stable requires little pilot attention after it is trimmed for a certain airspeed and power setting. Today’s post is excerpted from The Advanced Pilot’s Flight Manual by William Kershner.
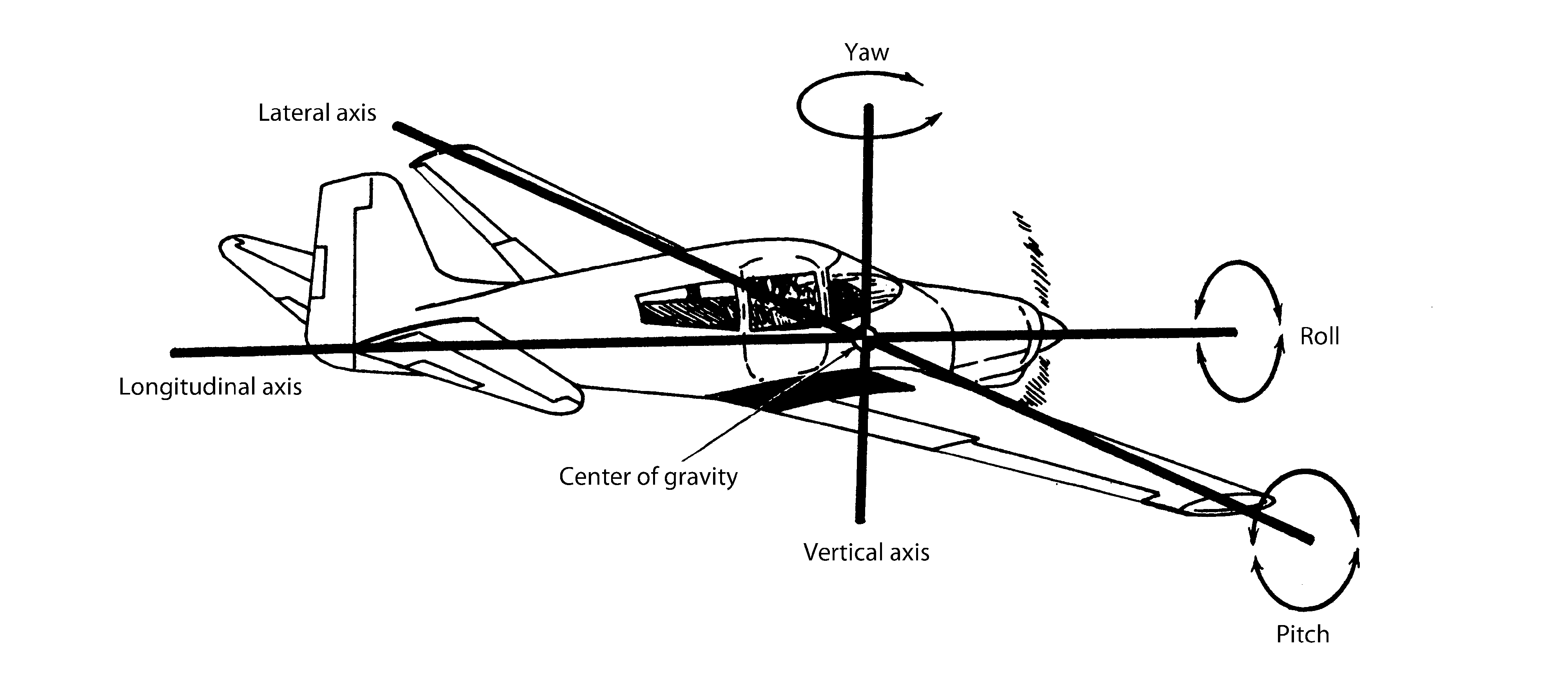
Figure 1. The three axes.
Stability, as defined by the dictionary, means “fixedness, steadiness, or equilibrium.” An object that is positively stable resists any displacement. One that is negatively stable does not resist displacement; indeed, it tends to displace itself more and more if acted upon by an outside force. An object that is neutrally stable doesn’t particularly care what happens to it. If acted on by a force it will move, but it does not tend to return to its position or to move farther after the force is removed.
Static Stability
Static (at rest) stability is the initial tendency of a body to return to its original position after being disturbed. An example of positive static stability is a steel ball sitting inside a perfectly smooth bowl. You can see that the ball has an initial tendency to return to its original position if displaced.
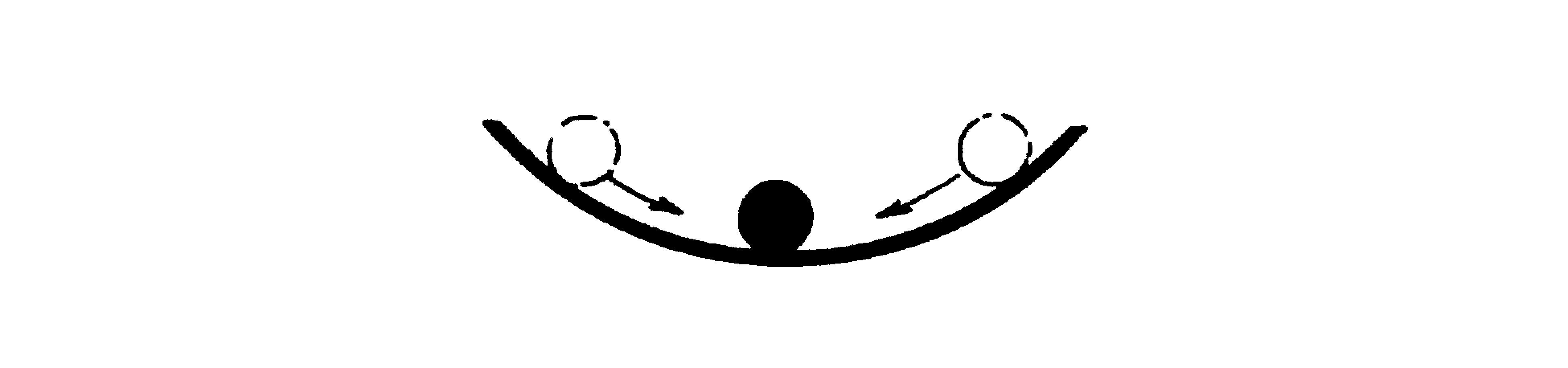
Figure 2. Positive static stability.
Figure 3 is an example of negative static stability. The ball is carefully balanced on the peak of the bowl, and the application of outside force results in its falling. It does not tend to return to its original position; on the contrary, it gets farther and farther from the original position as it falls.

Figure 3. Negative static stability.
Neutral static stability can be likened to a steel ball on a perfectly flat smooth surface. If a force is exerted on it, the ball will move and stop at some new point after the force is removed.
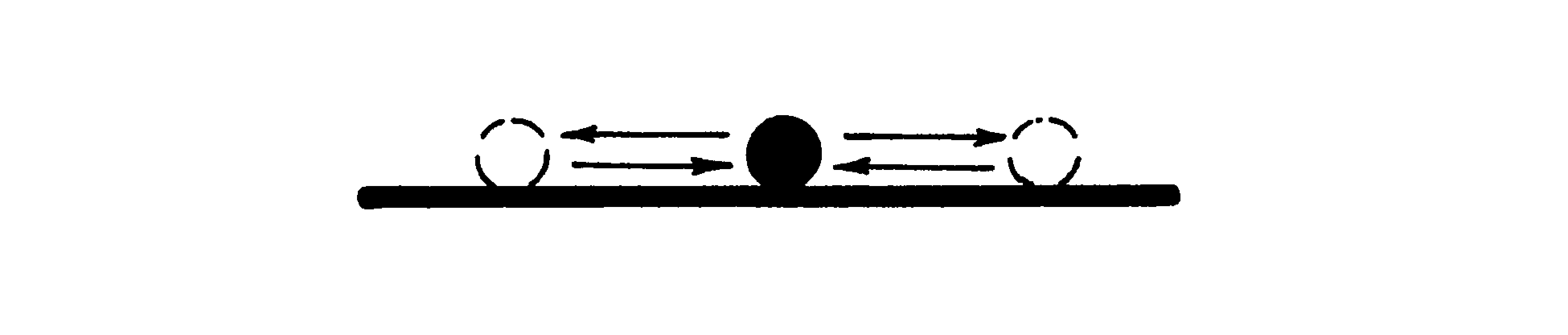
Figure 4. Neutral static stability.
Dynamic Stability
The actions a body takes in response to its static stability properties show its dynamic (active) stability. This dynamic stability usually is considered to be the time history of a body’s response to its inherent static stability.
Take the example of the steel ball and the bowl. Figure 2 shows that the ball, when inside, tends to stay in the center of the bowl—it has positive static stability. It requires force to displace it up the side, and it returns immediately to its original position.
Now suppose you push the steel ball well up the side of the bowl and quickly release it. The ball will roll toward the center position, overshoot, and return, keeping this up with ever shortening oscillations until finally it returns to rest in the center. The ball has positive static stability because it resists your pushing it up the side and has positive dynamic stability because its actions tend to return it to the original position. That is, the oscillations about its original position become less and less until it stops at the original point. This is called periodic motion; the ball makes a complete oscillation in a given interval of time or period. These periods remain approximately the same length (exactly the same under theoretical conditions) even though the amplitude (movement) is less and less.
You can also see periodic motion by suspending a heavy weight on a string, making a homemade pendulum. The pendulum at rest has positive static stability—it resists any attempt to displace it. It has positive dynamic stability in that it finally returns to its original position through a series of periodic oscillations of decreasing amplitude.
The ball in the bowl could be given the property of aperiodic (nontimed) positive dynamic stability by filling the bowl with a heavy liquid such as oil (Figure 5). The liquid would damp the oscillations to such an extent that the ball would probably return directly, though more slowly, to the original position with no overshooting and hence no periodic motion. Through manipulation of the system (adding oil), you have caused its motions to be aperiodic.
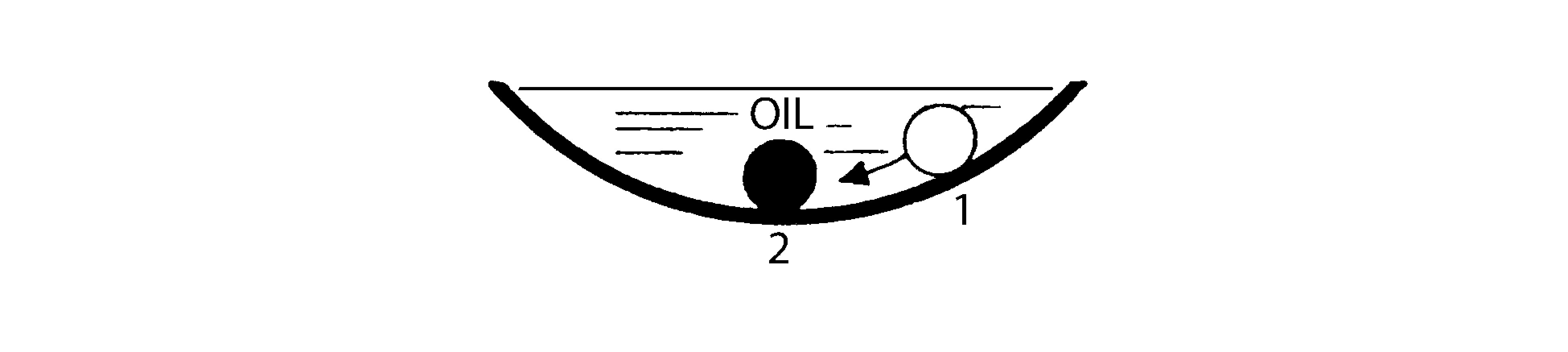
Figure 5. A periodic positive dynamic stability.
Unlike the steel ball inside the bowl, which is statically stable, resists any displacement, and has positive dynamic stability, a properly designed airplane does not necessarily have positive dynamic stability under all conditions (see the section, Longitudinal Dynamic Stability of the Airplane, later in this chapter). And the fact that an airplane sometimes has positive static stability does not mean that its dynamic stability is also positive. Outside forces may act on the airplane so that the oscillations stay the same or even become greater.
Back to the ball inside the bowl. Suppose you start the ball rolling and then rock the bowl with your hand so that the oscillations do not decrease. Because of the outside force you set up, the ball’s oscillations retain the same amplitude. The system has positive static stability but neutral dynamic stability—the ball’s oscillations continue without change. The airplane may also be affected by outside (aerodynamic) or inside (pilotinduced) forces that result in undiminishing oscillations, or neutral dynamic stability, even though it is properly balanced, or statically stable.
Now suppose you rock the bowl even more violently. The ball’s oscillations get greater and greater until it shoots over the side. You introduced an outside factor that resulted in negative dynamic stability—the oscillations increasing in size until structural damage occurred (the ball went over the side).
Thus, the system (or airplane) with positive static stability may have positive, neutral, or negative dynamic stability. A system that is statically stable will have some form of oscillatory behavior. This tendency may be so heavily damped (the oil in the bowl) that it is not readily evident. The oscillations show that the system is statically stable; the ball (or airplane) is trying to return to the original position. Outside forces may continually cause it to equally overshoot this position or may be strong enough to cause the oscillations to increase until structural damage occurs.
For a system that has neutral static stability such as a ball on a smooth flat plate, there are no oscillations because the ball isn’t trying to return to any particular position. It’s displaced and stays displaced.
A system that has negative static stability or is statically unstable (the terms mean t he same thing) will have no oscillations; there will be a steady divergence. Let’s use the ball and bowl again. This time turn the bowl over and balance the ball carefully on the peak (sure you can) and take another look at the statically unstable system (Figure 6).
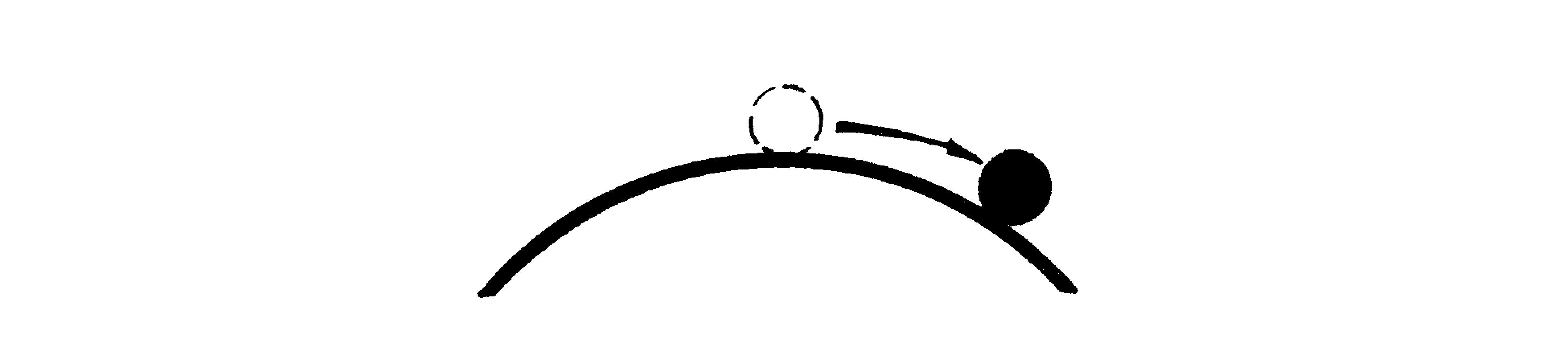
Figure 6. A statically unpredictable system.
If even a small force is applied, the ball rolls down the side of the bowl. The ball does not resist any force to offset it from its position—on the contrary, it wants to leave in the first place and when displaced leaves its original position at a faster and faster rate. There are no oscillations because there is no tendency to return at all. The statically unstable system has no dynamic (oscillatory) characteristics but continually diverges. The action this system takes in diverging is not always that simple, but that we’ll leave for the programmers. A statically stable system (or airplane) may have either positive, neutral, or negative dynamic stability characteristics.
We’ll show how this applies to you as a pilot in our next posts on aircraft performance.





