We’re devoting this week to aerodynamics, specifically the load factors experienced in turns. There’s more to turning your airplane than smoothly coordinating your ailerons and rudder pressure. Understanding the role of lift and gravity in a turn will help you fly efficiently and within the limitations of your airplane. The following is excerpted from William Kershner’s textbook The Student Pilot’s Flight Manual.
Lift is considered to act perpendicularly to the wingspan. Consider an airplane in straight and level flight where lift equals weight. Assume the airplane’s weight to be 2,000 pounds.
In Figure 1A everything’s great—lift equals weight. If the plane is banked is 60° as in Figure 1B, things are not so rosy. The weight’s value or direction does not change. It’s still 2,000 pounds downward. The lift, however, is acting at a different angle. The vertical component of lift is only 1,000 pounds, since the cosine of 60° is 0.500 (60° is used for convenience here; you certainly won’t be doing a bank that steep in the earlier part of your training). With such an unbalance, the plane loses altitude. The answer, Figure 1C, is to increase the lift vector to 4,000 pounds so that the vertical component is 2,000 pounds. This is done by increasing the angle of attack. Back pressure is applied to the elevators to keep the nose up.
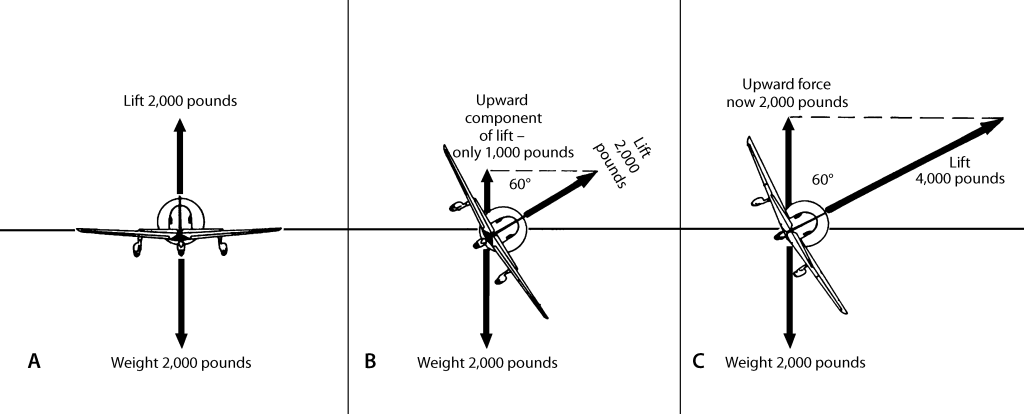
If in our example of the 60° bank, you roll out level but don’t get rid of the extra 2,000 pounds of lift you have, obviously the airplane will accelerate upward (the “up” and “down” forces will no longer be in balance). Maybe your idea of coordination is that demonstrated by a ballroom dancer, but it’s necessary in flying too. Think of control pressures rather than movement. The smoother your pressures, the better your control of the airplane.
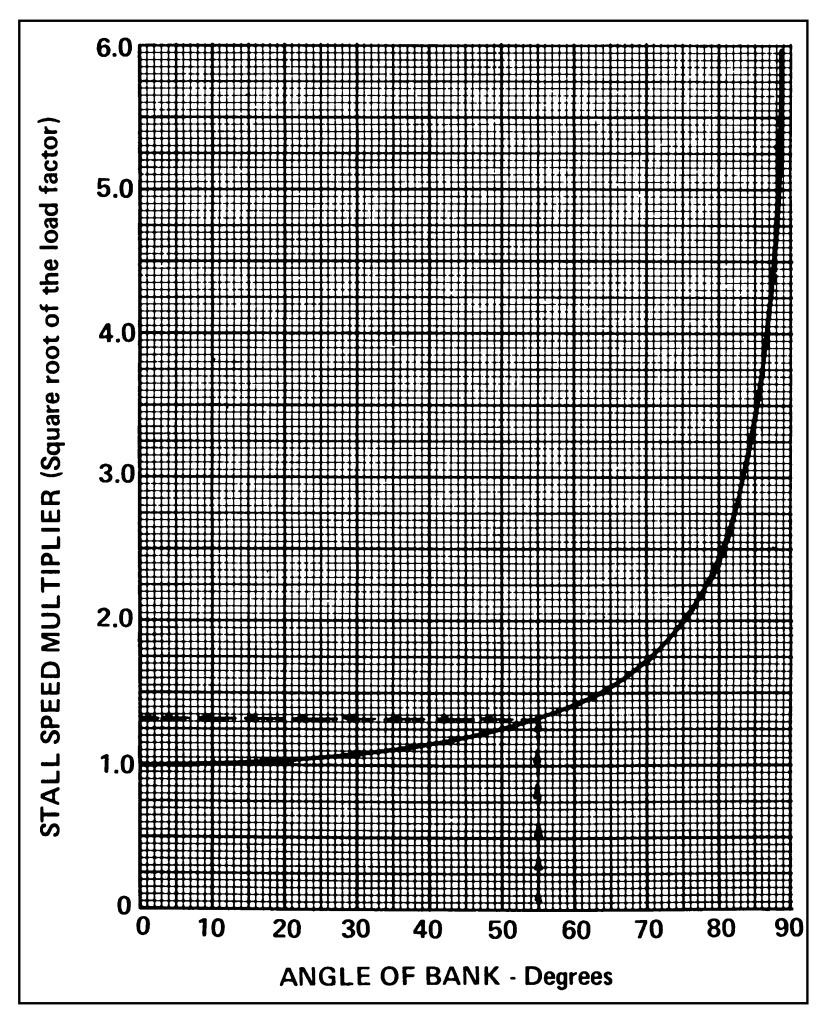
The turn introduces a new idea. It is possible to bank so steeply that the wings cannot support the airplane. The lift must be increased so drastically that the critical angle of attack is exceeded, and the plane stalls. In the previous example at 60° of bank, it was found that our effective wing area was halved; therefore, each square foot of wing area had to support twice its normal load. This is called a load factor of 2. A plane in normal, straight and level flight has a load factor of 1, or 1 “g.” You have this same 1 g load on your body at the time. Mathematically speaking, the load factor in the turn is a function of the secant of the angle of bank. The secant varies from 1 at 0° to infinity at 90°; so maintain altitude indefinitely in a constant 90° bank, an infinite amount of lift is required—and this is not available.
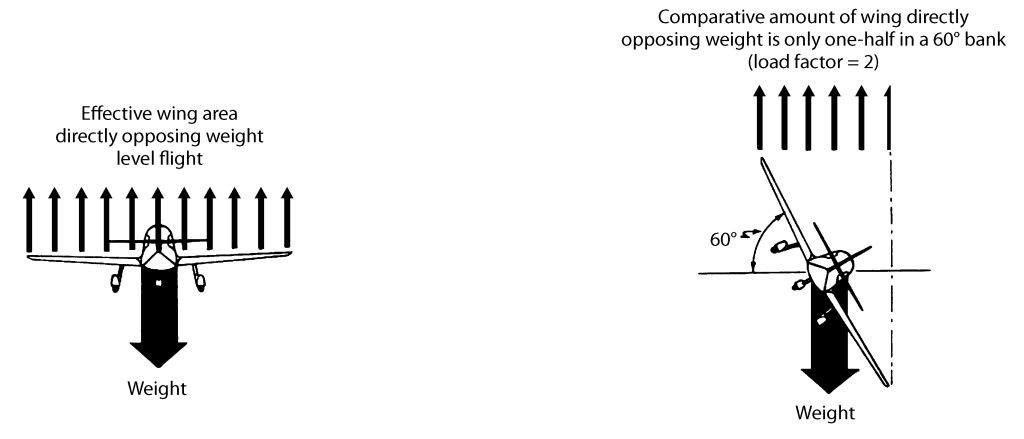
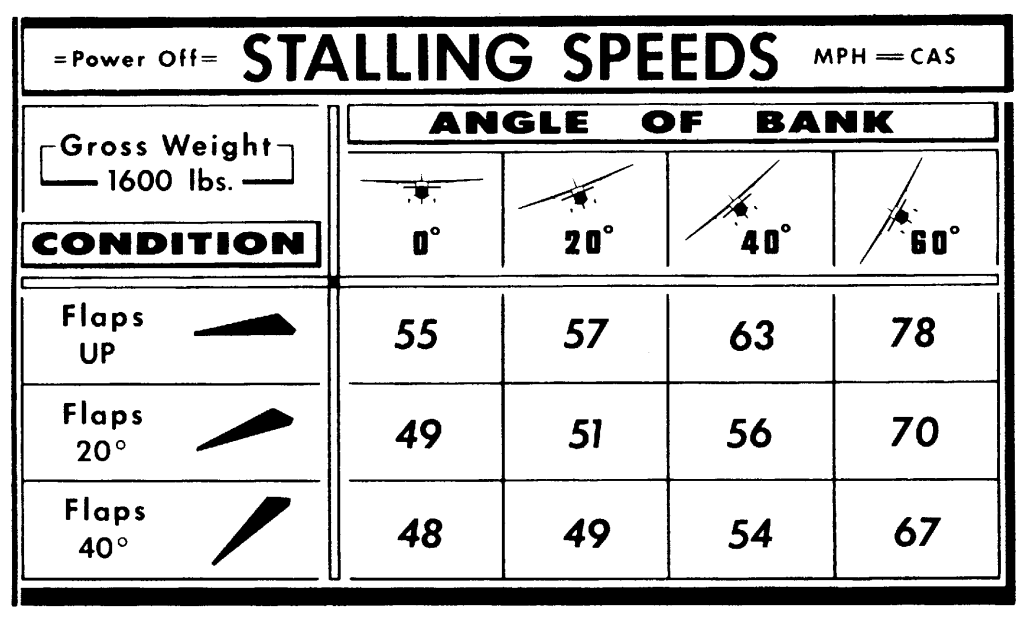
Putting it simply: The stall speed goes up in the constant altitude turn; and the steeper the bank, the faster the small speed jumps up, as can be seen in Figures 3 and 4. The load factors just discussed are “positive” load factors and are attained by pulling the wheel back, causing you to be pressed down in the seat. A negative load factor is applied if the control wheel is pushed forward abruptly, and in this case you feel “light” and tend to leave the seat. Lightplanes are generally stressed to take a maximum positive load factor varying from 3.8 to 6, and a negative load factor of between 1.52 and 3, depending on the make and model. Both you and the plane are able to stand more positive g’s than negative. Positive or negative load factors can be imposed on the plane by sharp up or down gusts as well as by the pilot’s handling of the elevators.